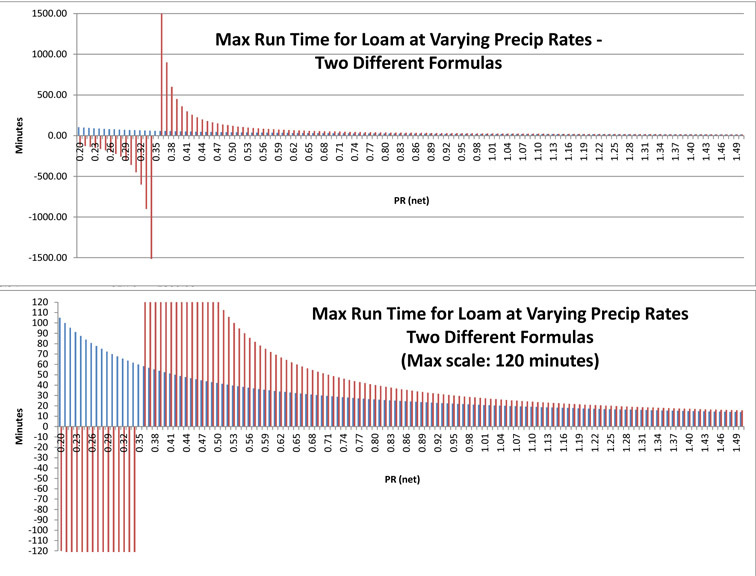
I’m pretty sure the documentation is wrong. It makes no sense to subtract ir from pr. We need a ratio here not a difference. So I’m going to assume that we should be dividing not subtracting.
As both values become closer to each other, then you produce a ratio closer to 1, so when they are the same, this division becomes idempotent, if you will.
So as The denominator approaches 1 the iro is allowed to apply water up to the asa as this formula indicates that no runoff is occurring as your absorption rate and your application rate are in sync, there is a minimum 30 minute soak period once asa is achieved (since asa will almost always be less than the application amount).
So going with hard numbers (but simple), to explain my reasoning, but I’m probably wrong. if you are somehow capable of putting together an irrigation system that can only apply .1 inch an hour, and you have your soil set to clay so your asa is set to .2, I would expect the iro to take 2 hours to apply water and a third hour for the asa to reduce to zero (because the second hour’s worth of water needs another hour to absorb) for your system to deliver .2 inches of water (see footnote 1). If the moisture level is being raised to 1 inch, you can see how you are going to,run away on time and require 14 hours (last hour gets an implied soak as the schedule is complete). Now, to really put anybody reading to sleep, if we doubled our pr to .2, then we get a ratio that equals 2, .2 / .1 = 2 as we would expect, because we have doubled our application rate so we should achieve asa in half the time, 1 hour, then 1 hour to soak, bringing our total time down to 9 hours.
But you can’t remove the asa as you have in the second graph as this value is directly inproportionate with slope, as slope increases Asa decreases and you run the risk of loosing water due to run off, especially as pr goes up. Thus you are only computing how much time the irrigation should run to put out all water, ignoring how much actually translocated into the ground.
Either way, we are all about to learn something. we will wait for the Emil or the franz to chime in, however, I would expect this curve to appear asymptotic (as pr goes up) as demonstrated by your graphs, so i think your data tables are generated correctly, just with an inaccurate denominator.
Edit: I’ll dig into your spreadsheet later, I have tried but it is brutal on my iPad.
Footnotes:
- Not sure if they wait for all water to be absorbed or if they wait for the previously applied amount to half absorb and divide Asa / 2 to absorb. Time could be saved with the ladder, I think?